This is a preprint of an article to appear in the journal Neurocomputing (Elsevier Science Ed.) in year 2000

L-Neuron: A Modeling Tool for the Efficient Generation and Parsimonious Description of Dendritic Morphology^

Giorgio A. Ascoli* and Jeffrey L. Krichmar

Krasnow Institute for Advanced Study at George Mason University, MS2A1

4400 University Dr., Fairfax, VA 22030-4444.

* Corresponding author. Tel. +1-703-993-4383; fax +1-703-993-4325. E-mail: ascoli@gmu.edu

^This work was supported in part by Human Brain Project grant R01-NS39600-01 by the National Institute of Neurological Disorders and Stroke (National Institutes of Health).

Abstract

We introduce L-Neuron (www.krasnow.gmu.edu/L-Neuron), a software package for the generation and study of anatomically accurate neuronal analogs. L-Neuron is based on sets of recursive rules that parsimoniously describe dendritic geometry and topology by locally inter-correlating morphological parameters (e.g. branch diameter and length). The L-Neuron algorithm stochastically samples parameter values from experimental statistical distributions, to generate multiple, non-identical virtual neurons within various morphological classes. Such neuronal structures, described by an L-system/Turtle graphic formalism, can be converted in various 3D-graphic formats and/or in compartmental anatomical files to be used in electrophysiological simulation studies with modeling programs such as Genesis or Neuron.

Author Biosketches

Giorgio A. Ascoli is a faculty member of the Krasnow Institute for Advanced Study and Visiting Assistant Professor in the Department of Psychology at George Mason University. He received his Ph.D. in biochemistry and neuroscience from the Scuola Normale Superiore of Pisa, Italy, and has a long-standing interest in the neurobiological basis of cognition. After several years of experimental work at the National Institutes of Health, Ascoli became interested in theoretical modeling and moved to Krasnow, where he leads the Computational Neuroanatomy Group.

Jeffrey L. Krichmar received a B.S. in Computer Science in 1983 from the University of Massachusetts at Amherst, a M.S in Computer Science from The George Washington University in 1991, and a Ph.D. in Computational Sciences and Informatics from George Mason University in 1997. Currently, he is a Junior Fellow in Theoretical Neurobiology at The Neurosciences Institute in San Diego, CA. His research interests include biologically plausible models of learning and memory and simulating the nervous system in a real-world artifact (“robot”) interacting with an environment.

1. Introduction and neuroanatomical background

In the past decade, the cellular behavior of several neuronal classes have been simulated in computer models that are extremely accurate in terms of physiological details (types and density of ionic channels, dendritic membrane properties, etc.).

Dendritic morphology is usually either taken straight from experimental data (anatomically precise compartmental models), or simplified with coarse approximations, or even neglected altogether, but it is rarely ever generated within the model in a biologically plausible way. This lack of neuroanatomical modeling is surprising in view of the general agreement among neuroscientists that dendritic morphology plays an important role in neuronal integration [1], and of the recent progress in computer graphics and 3D modeling applications. In this paper we introduce L-Neuron (LN), a software package for the generation and study of anatomically plausible neuronal analogs. The scientific literature offers a series of anatomical rules correlating local morphological parameters (e.g. branch diameter and length) that have proved to be powerful and parsimonious descriptors of specific aspects of dendritic topology [3,4,8,11-14]. LN integrates these successful correlations with global geometrical constraints. The LN implementation adopts a similar approach to Lindenmayer-systems, a well-known mathematical formalism particularly suitable to describe branching of plants, trees, fractals, and other recursive structures, and extensively developed in computer graphics [10].

Dendritic morphology can be characterized quantitatively at several levels. In a typical computer-acquired neuroanatomical file (such as in the Neurolucida format [6]), a single neuronal dendrite is described as a series of cylindrical compartments (“branches”). Each branch is represented in the file as a line containing a numerical tag, spatial Cartesian coordinates (x, y, and z), a diameter, and the tag of its “parent”, i.e. of the next branch in the path towards the soma. This “Cartesian” description constitutes a completely accurate description of dendritic morphology, but it is not compact and it bears little “intuitive” information for the user. In a classical neuroanatomical analysis, in contrast, neuronal dendrites are characterized on the basis of the statistical distributions of geometrical and topological parameters, such as bifurcation asymmetry or maximum branching order [14]. This level of description is intuitively more accessible to the neuroscientist, but, unlike the “Cartesian” format, it only yields information on the collective anatomy of a group of dendrites, i.e. it is not complete enough to provide a precise “blueprint” map of the original data. A third, intermediate level of description was first proposed by Hillman in the late seventies [8]. Hillman claimed that a small set of parameters, which he called “fundamental”, could be sufficient to describe completely and precisely an entire neuronal dendrite. This approach took advantage of a series of local correlations, such as Rall’s “power rule” linking the diameter of two daughter branches to the diameter of the bifurcating parent [11]. In Hillman’s description, a dendrite would start with a stem “initial diameter” (a fundamental parameter, thereafter marked in quotes in this paragraph). The stem would elongate for a certain “length”, and it would shrink according to a “taper rate”. If the branch diameter was greater than a certain “threshold”, the branch would then bifurcate yielding two new stems whose diameters would be completely determined by Rall’s “power” and by the daughter diameter “ratio”. The two daughter stems would continue the process as if they were new trees. If after elongation and tapering, a branch’s diameter fell below the “threshold” value, that branch would grow for an additional “terminal length” and then end. Hillman measured the fundamental parameters for several morphological classes, and reported results consistent with his analysis.

The importance of Hillman’s approach is that this description can be implemented in a self-consistent algorithm, i.e. a procedure by which a neuron can be “regenerated” from the correct values of fundamental parameters. In other words, a few parameters (as intuitive as in a classical anatomical analysis) are sufficient to describe the dendrite entirely (as completely and quantitatively as in a “Cartesian” file). Hillman suggested that the bifurcation angle could constitute an additional fundamental parameter to be measured from experimental data. In a modification of this algorithm, Tamori introduced the concept of “effective volume” to calculate the bifurcation angle from the other fundamental parameters [13].

In a third recursive algorithm, Burke and coworkers implicitly encoded the length of a branch in the probabilities to elongate or to bifurcate, and substituted Rall’s power constraint with the experimental distribution of daughter branch diameters [4]. To summarize, Hillman’s algorithm “calculates” diameters and “measures” angles; Tamori’s algorithm calculates both diameters and angles; and Burke’s algorithm measures both diameters and angles. LN implements all three such algorithms and adds two angular parameters (elevation and azimuth) to render branching three-dimensionally. In addition, LN adds a multiplicative term (i.e. a new fundamental parameter) to Rall’s power rule, as this modified equation was reported to fit better and more generally the experimental data from several morphological classes (e.g., [3]).

Burke’s algorithm describes the branch elongation process more accurately than the Hillman/Tamori approach. In the Hillman/Tamori description, branches are approximated as straight cylinders between two bifurcations. As a consequence, in virtual neurons generated with this algorithm, the dendritic pathlength is usually too short (if experimental branch lengths are measured as straight lines between bifurcation points), or the overall tree size is too large (if branch lengths are measured along the dendritic path). LN corrects this artifact by introducing a parameter of “segmentation”, that regulates the number of fragments constituting a branch between two bifurcation points, and whether their path is more straight or tortuous. Finally, LN adds the option of an external directional “bias” on the angles, called tropism [10]. Tropism is used in L-systems to simulate the effect of gravity or wind in growing botanical trees. In LN, tropism mimics the effect of neurotrophic factors, and can be either directional (along a certain vector), or centrifugal (e.g., dendrites growing preferentially away from the soma).

2.

Software development, system requirement, and source of experimental data

The L-Neuron program is written in plain “ANSI” C, and is highly portable. The results shown here were obtained on a Pentium PC under Windows 95. An identical version of LN has been compiled in a Unix environment (on an SGI Origin 200 under Irix 6.5). LN can run under DOS or in a Unix shell environment, and a user interface (programmed in Delphi) is available for Win95 (Fig. 1), based on a modification of the freeware program “Lsys32”. The LN source code is based on a modification of “L-parser”, a freeware application to generate L-systems, and the output of LN is a turtle graphic L-system string [10].

Although LN adopts the L-systems syntax, the implementation of sets of realistic neuroanatomical rules (similar to Hillman’s, Tamori’s, and Burke’s) instead of the L-systems rewrite rules constitutes a substantial improvement over previous attempts to describe neurons with L-systems [7]. LN reads a list of neuroanatomical parameters in the form of statistical distributions (truncated Gaussian with average, standard deviation, minimum; uniform within a range; or constant). When a virtual neuron is generated, actual values of the fundamental parameters are sampled stochastically from these distributions. LN-generated neurons can be displayed with the L-parser’s graphic extension “L-viewer” (Fig. 2), which allows 3D rendering and virtual fly-throughs of neurons. LN can convert files in several other graphic formats (bitmap, POV, DXF, VRML, Blob), as well as in the Cartesian neuroanatomical standard, which is compatible with Genesis [2], Neuron [9], ArborVitae [12], and CellViewer [5].

The neuroanatomical parameters used by LN can be obtained directly from the literature ([8], Table 1) or they can be measured from Cartesian files of experimental tracings. An alternative is to run a parameter search for a specific fundamental parameter to optimize the fit of other, non-fundamental parameters, if these are available through the literature or through experimental measurements.

Non-fundamental (or “emergent”) parameters are neuroanatomical parameters not used in the growth algorithm (for example, bifurcation asymmetry [14] and overall tree size). The availability of experimental Cartesian files remains the best source of data for neuroanatomical modeling. Several research groups have made their databases of neuronal tracings publicly available. One of the most extensive such archive, containing over 200 neurons from the rat hippocampus, is available electronically [5].

3. Discussion and Future Perspectives

L-Neuron provides a parsimonious description of neuroanatomical data and can generate sets of morphologically realistic cells for computer simulations of electrophysiology. LN uses experimental distributions of parameters from real-cell anatomical data to generate virtual neurons of various morphological classes. Within each class, the statistically constrained stochastic implementation of the algorithm produces multiple, non-identical neurons. The Purkinje cell shown in Fig. 2 is but one example of a set of similar Purkinje cells created with the same Hillman parameters. These virtual cells resemble the morphological class of the real Purkinje neurons from which the fundamental parameters were extracted.

It should be stressed that in LN a single set of parameters does not describe a single neuron, but rather a morphological class. Changing the statistical distributions of parameters will allow the same descriptive rules (e.g., Hillman’s algorithm) to generate neurons as diverse as Purkinje and pyramidal cells. We have so far applied the three LN algorithms to generate cerebellar Purkinje and stellate cells, cortical and hippocampal pyramidal cells, dentate gyrus granule cells, and spinal cord motoneurons. Once a single virtual neuron is generated with a given LN algorithm from a specific set of parameters, that neuron is constituted by its own individual set of branches in space, and can be downloaded in Cartesian format. Therefore, neurons from an experimental archive and virtually generated models can be compared visually and quantitatively (Fig. 3). A general strategy can be thus formulated to improve the available neuroanatomical algorithms and obtain more accurate models (Fig. 4). A set of real neurons belonging to a certain morphological class is the starting point to measure the statistical distributions of fundamental parameters of that class. One of the LN algorithms is then used to generate a set of virtual neurons, and a series of emergent parameters are measured from both the experimental neurons and the LN-generated virtual neurons. Emergent parameters will also consist of statistical distributions. A quantitative and visual comparison of virtual and real neurons is used to evaluate the correctness of the algorithm and provides insight on the anatomical process. Generating complete models of dendritic geometry in virtual reality thus also stimulates the development of analytical strategies to test whether the virtual neurons are morphologically equivalent to the real ones.

The generation of sets of virtual neurons is biologically relevant because it discriminates between important morphological parameters and emergent byproducts, which represent redundancies. If the algorithm produces accurate structures, it must contain all the required information and thus completely describes the original morphological family. In this case, a great deal of data compression is achieved, because thousands of neurons from one morphological class (occupying MB of computer memory in Cartesian format) could be described effectively and completely with a few lines of statistical distributions of LN parameters. At the same time, LN allows a form of data amplification, because, starting from a few hundred experimentally traced neurons, an arbitrarily large number of virtual neurons belonging to the corresponding morphological class can be generated. Therefore, we submit that LN can become a useful tool for the creation and maintenance of a large database of mammalian single-cell neuroanatomy.

In conclusion, the LN project has shown that the L-system formalism is suitable to implement the recursive algorithms available in the neuroanatomical literature for describing dendritic trees with a limited number of local parameters. LN is now being expanded to measure fundamental parameters directly from anatomical files and to evaluate automatically which algorithm best fits the source data. A complete analysis of neurons generated with the three LN algorithms will assess their applicability to various morphological classes. In addition, the influence of global parameters, such as tropism [10], is being evaluated, and other variations of neuroanatomical rules will be investigated. The limitation of L-Neuron consists in being oriented toward single-cell analysis, thus making it less suitable for studying the effect of neuronal morphology on network connectivity. However, the simplicity of this system also represents an important advantage because it allows the analysis of the influence of specific intrinsic and extrinsic determinants on neuronal shape, and consequently on neuronal electrophysiology. We believe that this package, portable to all major platforms and freely distributed, will further neuroanatomy, computational modeling, and scientific education. The reference URL for LN (with information on version release, virtual databases, and complete neuroanatomical analyses grouped by morphological classes) is: http://www.krasnow.gmu.edu/L-Neuron (case sensitive).

Acknowledgements. We are indebted to Laurens Lapré for making the L-parser source code available to us. The L-parser/L-viewer package is available at: http://www.xs4all.nl/~ljlapre

. We warmly thank Dr. Larry Hunter for first suggesting to us the use of L-systems to describe dendritic morphology, and for many useful discussions. We gratefully acknowledge Chris Lichti for adapting his Lsys user interface (http://www.mindspring.com/~chlichti/html/lsys32.html) to LN. Our gratitude is extended to Dr. Slawomir Nasuto for critically reviewing this manuscript.

References

[1] GA Ascoli, Progress and perspective in computational neuroanatomy, Anat. Rec. (New Anat.), In Press, Dec 1999.

[2] JM Bower, D Beeman, The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System (Springer-Verlag, New York, 1998)

[3] RE Burke, S Cullheim, JW Fleshman, LL Glenn, Dendritic morphology of type-identified a-motoneurons in the cat, in: RJ Lasek and MM Black, eds., Intrinsic determinants of neuronal form and function (Liss, New York, 1988) 167-176

[4] RE Burke, WB Marks, B Ulfhake, A parsimonious description of motoneurons dendritic morphology using computer simulation, J. Neurosci. 12 (1992) 2403-2416

[5] RC Cannon, DA Turner, GK Pyapali, HV Wheal, An on-line archive of reconstructed hippocampal neurons, J. Neurosci. Methods 84 (1998) 49-54

[6] JR Glaser, EM Glaser, Neuron imaging with Neurolucida - a PC-based system for image combining microscopy, Comput. Med. Imaging Graph. 14 (1990) 307-317

[7] P Hamilton, A language to describe the growth of neurites, Biol. Cyber. 68 (1993) 559-565

[8] DE Hillman, Neuronal shape parameters and substructures as a basis of neuronal form, in: F Schmitt, ed., The neurosciences, 4th study program (MIT Press, Cambridge, 1979) 477-498

[9] ML Hines, NT Carnevale, The NEURON simulation environment, Neural Comput. 9 (1997) 1179-1209

[10] P Prusinkiewicz, A Lindenmayer, The Algorithmic Beauty of Plants (Springer-Verlag, New York, 1990)

[11] W Rall, Branching dendritic trees and motoneurons membrane resistivity, Exptl. Neurol. 1 (1959) 491-527

[12] SL Senft, GA Ascoli, Reconstruction of brain networks by algorithmic amplification of morphometry data, Lecture Notes Computer Science 1606 (1999) 25-33.

[13] Y Tamori, Theory of dendritic morphology, Phys. Rev. E 48 (1993) 3124-3129

[14] WH Verwer, J van Pelt, Descriptive and comparative analysis of geometrical properties of neuronal tree structures, J. Neurosci. Meth. 18 (1986) 179-206

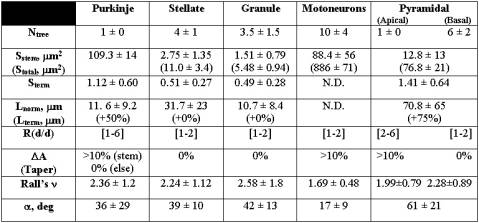
Table 1: Statistical distributions of Hillman’s fundamental parameters for several morphological classes [8]. The values for the number of trees (N), branch section area (S), branch length (L), daughter diameter ratio (R), taper (DA), Rall’s power (n), and bifurcation angle (a) are reported as normal (mean±standard deviation) or uniform ([range]) distributions .

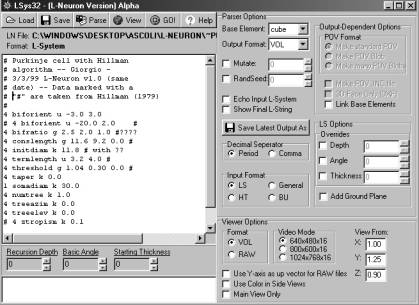
Fig.1: A screenshot from the L-Neuron user interface (Windows95/98). The left window is a text editor that allows the user to insert or modify parameter settings. The right panel controls the options for the type of algorithm, download format, random seed, and display settings.

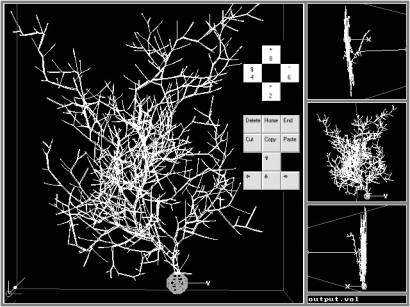
Fig. 2: An LN-generated Purkinje cell displayed with L-viewer (Dos/Windows). This virtual neuron (created with Hillman’s algorithm) can be moved, oriented and zoomed through simple key strokes. The right insets represent views from the top (top), front (middle) and side (bottom).

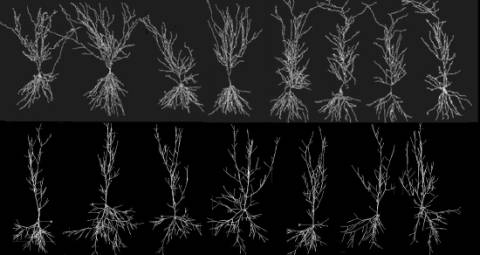
Fig. 3: Real hippocampal pyramidal cells (top) obtained from an experimental archive [5] are used to extract fundamental parameters and generate virtual neurons (bottom), with Tamori’s algorithm. No two virtual or real neurons are ever identical, though they clearly belong to a recognizeable morphological class.

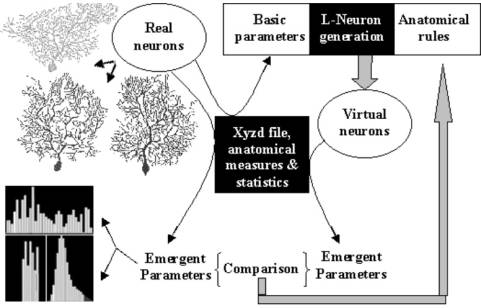
Fig. 4: The strategy to search for the most accurate neuroanatomical description, starting from available algorithms. Fundamental (or basic) parameters are measured from real neurons and fed into L-Neuron to generate virtual neurons. Emergent parameters are measured from both real and virtual neurons. The comparison between the two sets of statistical distributions suggests the appropriate modifications of the anatomical rules, and the process is then reiterated (after [12]).